De l’équilibre et de la composition des forces qui agissent sur un point matériel.
1. Un corps nous paroît se mouvoir, lorsqu’il change de situation par rapport à
un système de corps que nous jugeons en repos; mais comme tous les corps, ceux
même qui nous semblent jouir du repos le plus absolu, peuvent être en mouvement;
on imagine un espace sans bornes, immobile et pénétrable à la matière: c’est aux
parties de cet espace réel ou idéal, que nous rapportons par la pensée,
la position des corps, et nous les concevons en mouvement, lorsqu’ils répondent
successivement à divers lieux de l’espace.
1. A body appears to us to be in motion, when it changes its relative situation
with respect to a system of bodies supposed to be at rest ; but as all bodies,
even those which appear in the most perfect repose, may be in motion; a space is
conceived of, without bounds, immoveable, and penetrable by the particles of
matter; and we refer in our minds the position of bodies to the parts of this
real, or ideal space, supposing the bodies to be in motion, when they
correspond, in successive moments, to different parts of this space.
La nature de cette modification singulière, en vertu de laquelle un
corps est transporté d’un lieu dans un autre, est et sera toujours
inconnue ; on l’a désignée sous le nom de force; on ne peut
déterminer que ses effets et les loix de son action. L’effet d’une
force agissante sur un point matériel, est de le mettxe en mouvement,
si rien ne s’y oppose; la direction de la force est la droite qu’elle
tend à lui faire décrire. Il est visible que si deux forces agissent
dans le même sens, elles s’ajoutent l’une à l’autre, et que si elles
agissent en sens contraire, le point ne se meut qu’en vertu de leur
différence. Si leurs directions forment un angle entre elles, il en
résulte une force dont la direction est moyenne entre celles des
forces composantes. Voyons quelle est cette résultante et sa
direction.
The nature of that singular modification, by means of which a body is
transported from one place to another, is now, and always will be, unknown; it
is denoted by the name of Force. We can only ascertain its effects, and the
laws of its action. The effect of a force acting upon a material point, or
particle, is to put it in motion, if no obstacle is opposed; the direction of
the force is the right line which it tends to make the point describe. It is
evident, that if two forces act in the same direction, the resultant is the sum
of the two forces; but if they act in contrary directions, the point is affected
by the difference of the forces. If their directions form an angle with each
other, the force which results will have an intermediate direction between the
two proposed forces. We shall now investigate the quantity and direction of
this resulting force.
Pour cela, considérons deux forces \(x\) et \(y\) agissantes à-la-fois sur
un point matériel \(M\), et formant entre elles un angle droit. Soit
\(z\) leur résultante, et \(\theta\) l’angle qu’elle fait avec la
direction de la force \(x\); les deux forces \(x\) et \(y\) étant données,
l’angle \(\theta\) sera déterminé, ainsi que la résultante \(z\), en sorte
qu’il existe entre les trois quantités \(x\), \(z\) et \(\theta\), une
relation qu’il s’agit de connoître.
For this purpose, let us consider two forces, \(x\) and \(y\), acting at the same
moment upon a material point \(M\), in directions forming a right angle with each
other. Let \(z\) be their resultant, and \(\theta\) the angle which it makes with
the direction of the force \(x\). The two forces \(x\) and \(y\) being given, the
angle \(\theta\) and the quantity \(z\) must have determinate values, so that there
will exist, between the three quantities \(x\), \(z\) and \(\theta\), a relation which
is to be investigated.
Supposons d’abord les forces \(x\) et \(y\) infiniment
petites, et égales aux différentielles \(dx\) et \(dy\); supposons
ensuite que \(x\) devenant successivement \(dx\), \(2dx\), \(3dx\), &c. \(y\)
devienne \(dy\), \(2dy\), \(3dy\), &c., il est clair que l’angle \(\theta\)
sera toujours le même, et que la résultante \(z\) deviendra
successivement \(dz\), \(2dz\), \(3dz\), &c.; ainsi dans les accroissemens
successifs des trois forces \(x\), \(y\) et \(z\), le rapport de \(x\) à \(z\)
sera constant, et pourra être exprimé par une fonction de \(\theta\),
que nous désignerons par \(\varphi\left(\theta\right)\); on aura donc
\(x=z\mathord.\varphi\left(\theta\right)\), équation dans laquelle on
peut changer \(x\) en \(y\), pourvu que l’on y change semblablement
l’angle \(\theta\) dans \(\frac{\pi}{2}-\theta\), \(\pi\) étant la
demi-circonférence dont le rayon est l’unité.
Suppose in the first place that the two
forces \(x\) and \(y\) are infinitely small, and equal to the
differentials \(dx\), \(dy\). Then suppose that \(x\) becomes successively
\(dx\), \(2\,dx\), \(3\,dx\), &c., and \(y\) becomes \(dy\), \(2\,dy\), \(3\,dy\),
&c., it is evident that the angle \(\theta\) will remain constant, and
the resultant \(z\) will become successively \(dz\), \(2\,dz\), \(3\,dz\),
&c., and in the successive increments of the three forces \(x\), \(y\) and
\(z\), the ratio of \(x\) to \(z\) will be constant, and may be expressed by
a function of \(\theta\), which we shall denote by \(\varphi(\theta)\);
* we shall therefore have \(x = z\mathord{.}\varphi(\theta)\), in
which equation we may change \(x\) into \(y\), provided we also change the
angle \(\theta\) into \(\frac{\pi}{2}-\theta\),
\(\theta\)
\(\pi\) being the semi-circumference of a circle whose radius is unity.
* Bowditch footnote: (1) A quantity \(z\) is said to be a function of
another quantity \(x\), when it depends on it in any manner. Thus, if
\(z\), \(y\) \(x\)
be variable, \(a\), \(b\), \(c\), &c. constant, and we have either of the
following expressions, \(z=ax+b\), \(z=ax^2+bx+c\); \(z=a^x\), \(z=\sin ax\),
&c. \(z\) will be a function of \(x\); and if the precise form of the
function is known, as in these examples, it is called an explicit
function. If the form is not known, but must be found by some
algebraical process, it is called an implicit function.
Maintenant, on peut considérer la force \(x\) comme la résultante
de deux forces \(x’\) et \(x''\) dont la première \(x'\) est dirigée suivant la
résultante \(z\), et dont la seconde \(x''\) est perpendiculaire à cette résultante.
Now we may consider the force \(x\) as the resultant of two forces \(x'\)
and \(x''\), of which the first \(x'\) is directed along the resultant
\(z\), and the second \(x''\) is perpendicular to it. †
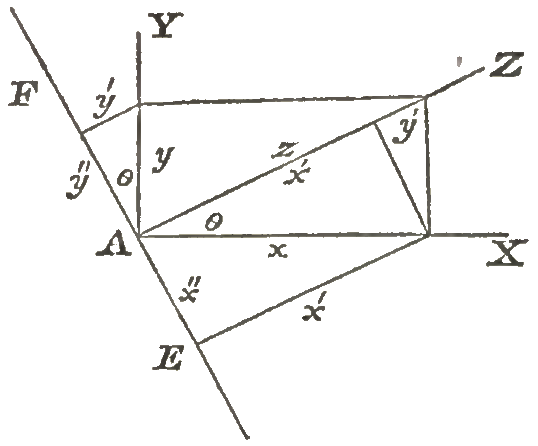
† Bowditch footnote: (2) For illustration, suppose the forces \(x\) and \(y\) to act at the
point \(A\), in the directions \(A\,X\), \(A\,Y\), respectively, and that
the resultant \(z\) is in the direction \(A\,Z\), forming with \(A\,X\),
\(A\,Y\), the angles \(Z\,A\,X=\theta\), \(Z\,A\,Y=\frac{\pi}{2}-\theta\).
Then as above, we have \(x=z\mathord{.}\varphi(\theta)\),
\(y=z\,\varphi\left(\frac{\pi}{2}-\theta\right)\). Draw \(E\,A\,F\)
perpendicular to \(A\,Z\), and suppose the force \(x\) in the direction
\(A\,X\) to be resolved into two forces, \(x'\), \(x''\) in the directions
\(A\,Z\), \(A\,E\), respectively, so that the angle \(Z\,A\,X=\theta\), and
\(X\,A\,E = \frac{\pi}{2}-\theta\). Then, in the same manner in which
the above values of \(x\), \(y\), are obtained from \(z\), we may get \(x'=
x.\varphi\left(\theta\right)\);
\(x''=x.\varphi\left(\frac{\pi}{2}-\theta\right)\). If in these we
substitute the values \(\varphi\left(\theta\right)=\frac{x}{z}\);
\(\varphi\left(\frac{\pi}{2}-\theta\right) = \frac{y}{z}\), deduced from
the above equations, we obtain \(x'= \frac{x^2}{z}\);
\(x''=\frac{xy}{x}\). In like manner, if the force \(y\), in the
direction \(A\,Y\), be resolved into the two forces \(y'\), \(y''\), in the
directions \(A\,Z\), \(A\,F\), making the angle
\(Y\,A\,Z=\frac{\pi}{2}-\theta\), \(Y\,A\,F=0\), we shall have
\(y'=y.\varphi\left(\frac{\pi}{2}-\theta\right)\);
\(y''=y.\varphi\left(\theta\right)\); which, by substituting the above
values of \(\varphi\left(\frac{\pi}{2}-\theta\right)\),
\(\varphi\left(\theta\right)\) become \(y'=\frac{y^2}{z}\),
\(y''=\frac{xy}{z}\), as above.
La force \(x\) qui résulte de ces deux nouvelles forces, formant l’angle \(\theta\)
avec la force \(x'\), et l’angle \(\frac{\pi}{2}-\theta\) avec la force \(x''\), on
aura \[x'=x\mathord.\varphi\left(\theta\right)=\frac{x^2}{z};\quad
x''=x\mathord.\varphi\left(\frac{\pi}{2}-\theta\right) = \frac{xy}{z};\] on peut
donc substituer ces deux forces, à la force \(x\). On peut substituer
pareillement à la force \(y\), deux nouvelles forces \(y'\) et \(y''\) dont la
première est égale à \(\frac{y^2}{z}\) et dirigée suivant \(z\), et dont la seconde
est égale à \(\frac{xy}{z}\), et perpendiculaire à \(z\); on aura ainsi, au lieu des
deux forces \(x\) et \(y\), les quatre suivantes: \[\frac{x^2}{z}, \frac{y^2}{z},
\frac{xy}{z}, \frac{xy}{z};\] les deux dernières agissant en sens contraire, se
détruisent; les deux premières agissant dans le même sens, s’ajoutent et forment
la résultante \(z\); on aura donc \[x^2+y^2=z^2;\] d’où il suit que la résultante
des deux forces \(x\) et \(y\) est représentée pour la quantité, par la diagonale du
rectangle dont les côtés représentent ces forces.
The force \(x\), which results from these two new forces, forms the
angle \(\theta\) with the force \(x'\), and the angle
\(\frac{\pi}{2}-\theta\) with the force \(x''\); we shall therefore have
\[x'=x\,\varphi\left(\theta\right)=\frac{x^2}{z};\quad
x''=x\,\varphi\left(\frac{\pi}{2}-\theta\right) = \frac{xy}{z};\] and we
may substitute these two forces instead of the force \(x\). We may
likewise substitute for the force \(y\) two new forces, \(y'\) and \(y''\),
of which the first is equal to \(\frac{y^2}{z}\) in the direction \(z\),
and the second equal to \(\frac{xy}{z}\) perpendicular to \(z\); we shall
thus have, instead of the two forces \(x\) and \(y\), the four following:
\[\frac{x^2}{z}, \frac{y^2}{z}, \frac{xy}{z}, \frac{xy}{z};\] the two
last, acting in contrary directions, destroy each other; * the two
first, acting in the same direction, are to be added together, and
produce the resultant \(z\); we shall therefore have †
\[x^2+y^2=z^2;\]
whence it follows, that the resultant of the two forces \(x\) and \(y\) is
represented in magnitude, by the diagonal of the rectangle whose sides
represent those forces.
* Bowditch footnote: (3) For, by the preceding note, the force \(x''=\frac{xy}{z}\), is in the
direction \(A\,E\), and the force \(y''=\frac{xy}{z}\), is in the opposite
direction \(A\,F\), and as they are equal they must destroy each other.
† Bowditch footnote: (4) The sum of the two forces \(x'=\frac{x^2}{z}\), \(y'=\frac{y^2}{z}\) in the
direction \(A\,Z\), being put equal to the resultant \(z\), gives
\(\frac{x^2}{z}+\frac{y^2}{z}=z\), which multiplied by z becomes \(x^2+y^2=z^2\).
Let us now determine the angle \(\theta\). If we increase the force \(x\) by the
differential \(dx\), without varying the force \(y\), that angle will be diminished
by the infinitely small quantity \(d\theta\); * now we may conceive the force
\(dx\) to be resolved into two other forces, the one \(dx'\) in the direction \(z\),
and the other \(dx''\) perpendicular to \(z\); the point \(M\) will then be acted upon
by the two forces \(z+dx'\) and \(dx''\), perpendicular to each other, and the
resultant of these two forces, which we shall call \(z'\) will make with \(dx''\)
the angle \(\frac{}{}-d\theta\); † we shall thus have, by what precedes,
\[dx''=z'\mathord.\varphi\left(\frac{\pi}{2}-d\theta\right);\] consequently the
function \(\varphi\left(\frac{\pi}{2}-d\theta\right)\) is infinitely small, and of
the form \(-kd\theta\), \(k\) being a constant quantity, independent of the angle
\(\theta\); ‡ we shall therefore have